유클리드 호제법(Euclidean algorithm)

최대공약수와 최소공배수 구하기

 

최대공약수와 최소공배수는 수학의 기초 중 기초라고 할 수 있을 정도로 널리 알려진 개념이다.

다음 이미지를 예시로 보자

 

 

상위의 숫자를 공통적으로 2로 나눌 수 있다.그 다음에도 2로 나눌 수 있다. 하지만 맨 하단에 있는

5, 6, 9는 공통적으로 나눌 수 없다. 이 때 2 X 2 를 한 값인 4가 최대 공약수가 되는 것이다.

 

유클리드 호제법

최대 공약수

 

최대공약수를 구하기 가장 쉬운 방법이 유클리드 호제법이다.

 

정의는 다음과 같다. 

 

"2개의 자연수 a,b (a > b)에 대해서 a를 b로 나눈 나머지가 r일 때, a와 b의 최대공약수는 b와

r의 최대공약수와 같다."

 

예를 들어보자 

두 수 a(270)과 b(192)가 있다. 큰 수에서 작은 수로 MOD(나머지 연산)을 수행한다.

 

● 270(a) % 192(b) = 78이다. 그 후 b였던 192가 a가 되는 것이고 연산의 값인 78이 b가 된다.

● 192(a) % 78(b) = 36이다. 그 후를 반복하면

                .

                .

                .

● 36(a) % 6(b) 은 0이 된다. 그럼 이 때 마지막 b값이 최대 공약수가 되는 것이다.

 

최소 공배수

 

최소 공배수는 초기의 a X b / 최대공약수이다. 즉 270 * 192 / 6의 값인 8640이 된다.

 

그렇다면 3개 이상의 값은?

맨 위의 그림을 다시 보자

3개의 이상 유클리드

 

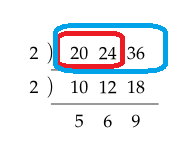
간단하다. 최대 공약수를 구하려면 빨간색의 최대 공약수와 마지막 값과 최대 공약수를 구하면되고

최고 공배수를 구하려면 빨간색의 최소 공배수와 마지막 값의 최소 공배수를 구하면 된다.

 

3개 이상의 경우는 이를 반복하면 된다.